Hydraulic design of side-ported RO vessel arrangement is where many manufacturers stumble over and over again. Generally any RO vessels arrangement has two primary elements: the vessel row and the pipe manifolds (Fig.1), From hydraulics point of view the side-ported vessels and pipe manifolds may be connected in a number of ways

Fig.1 Three side-ported vessels in a row
Fig.2 Hydraulic classification of the side-ported vessels and pipe manifolds connections (in clockwise direction): 1. S-type row; 2. U-type row; 3. S-type manifold; 4. U-type manifold;
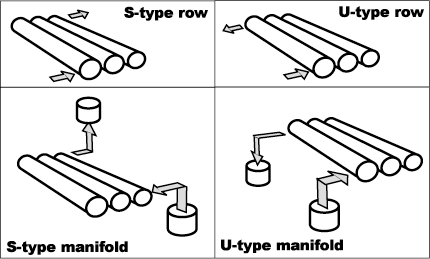
In the S-type row of vessels the feed inlet and brine outlet for the row are in the opposite vessels. For U-type row the feed inlet and the brine outlet are in the same vessel. The former type is rarely used.
The S-type and U-type manifold arrangements consider the feed and brine streams distribution to the vessel rows and collection from the rows. In the S-type manifold connection to the vessel rows the feed and brine streams in the dividing and collecting manifolds are in the same direction. In the U-type manifold connection the afore-mentioned streams are in opposite directions (Fig.2).
In designing the vessel arrangement three hydraulic phenomena shall be taken into account.
- Pressure losses in connections of vessels and manifolds,
- The feed flow maldistribution between the vessels in the same row,
- The feed flow maldistribution between the vessel rows connected to the same dividing and collecting manifolds.
The pressure losses in the feed and brine streams have direct effect on the process energy consumption and productivity. They can’t be neglected even at the preliminary design stage of the RO desalination unit as the loss in production may be surprisingly high - up to 3…8%.
The flow maldistribution may be measured by the ratio of minimum flow rate of the feed trough the vessel to the feed flow maximum value. For example, in the U-type row the first vessel accepts the maximum fed flow, while the vessel farthest from the manifold receives the minimum flow.
In the U-type manifold the picture is quite the opposite: the row nearest to the inlet receives the minimum feed flow rate. This behavior is inherent and has a theory-grounded explanation. In a dividing manifold, the flow diverted to the vessel causes the main stream to decelerate and its static pressure to increase stepwise. Thus, the pressure drop across the vessel row increases progressively with its distance from the inlet. This results in hydraulic non-uniformity with the maximum flow in the row farthest from the manifold inlet. In a combining manifold, the velocity in the main stream increases as the branch streams from the vessel rows progressively merge into it. It causes the static pressure in the manifold to drop downstream, its minimum being at the manifold outlet. Minimum and maximum pressure areas in both manifolds define extreme flows through the vessels. Generally the S-type manifolds perform better than the U-type ones.
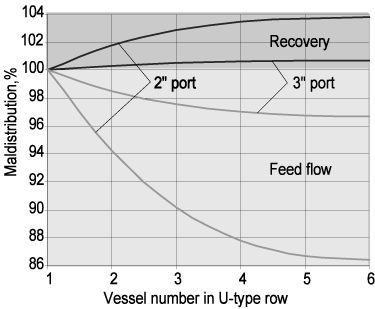 The feed flow maldistribution results in the recovery maldistribution working in the opposite direction; the higher the flow rate the lower the recovery. Fig. 3 gives fair indication of the predicted maldistribution effect in a row containing 6 vessels. Two cases are compared - the 2-inch and 3-inch side ports for feed and brine.
The feed flow maldistribution results in the recovery maldistribution working in the opposite direction; the higher the flow rate the lower the recovery. Fig. 3 gives fair indication of the predicted maldistribution effect in a row containing 6 vessels. Two cases are compared - the 2-inch and 3-inch side ports for feed and brine.
Fig.3 The vessel feed flow rate and membrane recovery maldistribution in the U-type row for seawater of 62 Bar, at the maximum permeate flux of 27 l/(m2*h), recovery of 45%, and fouling of 80%.
In hydraulically faulty designs the flow maldistribution may reach 15% (abs), the maximum recovery maldistribution being below 5%. It leads to a less effective usage of the RO membranes and shortens their life.
To limit the extents of the "in-row" maldistribution phenomenon the maximum number of vessels in a row shall be limited to the figures given in Table 1
Table 1 Maximum number of vessels in a single row
| port size | 1.5" | 2" | 2.5" | 3" |
| Sea Water | 1 | 3 | 4 | 7 |
| Brackish Water | 1 | 2 | 3 | 5 |
For brackish water desalination at the recovery above 65% the brine discharge connection size may be reduced as compared to the feed connection size. Fewer vessels in a row for brackish water is explained by much higher permeate fluxes in membranes and feed flow rates to each membrane.
To keep at bay the "in-manifold" maldistribution phenomenon (in practice less than 5%), the manifold design with multiple rows should meet the following conditions.
Where dport, Dmanifold - the port and manifold inner diameters, rows - total number of rows (on both sides of the pipe manifold if symmetrically located). From equation (1) it follows, that at the total number of rows equal 30 the manifold diameter should be at least 5 times bigger than the port size.
If the above hydraulic design criteria (of table 1 and equation 1) are met, the only issue to be tackled with is the pressure loss calculation in a vessel row.
Two approaches may be used for pressure loss calculation in a vessel row. One is based on successive step-by-step calculation of all the vessels starting from the vessel farthest from the pipe manifold. It uses the membrane data and the pressure loss curves given in Fig.4 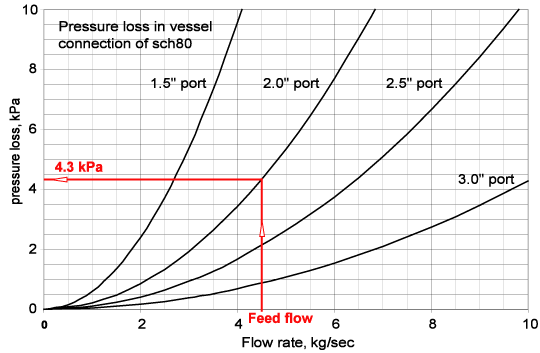
Fig.4 - Pressure loss in the "vessel-vessel" or "manifold-vessel" connection
This procedure requires special numeric algorithms and a sure choice for software programs.
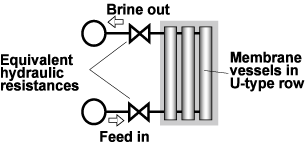
Fig.5 - Hydraulic model for pressure loss prediction in the U-type rows
The other approach considers the vessel row as some black box without internal pressure losses. The hydraulic model suggested for quick pressure loss prediction in the U-type rows is shown in Fig.5. In this model all pressure losses are applied to only 2 points - the feed inlet and the brine outlet. The equivalent hydraulic resistances are depicted below as valves. As known, pressure loss in a valve is described by the flow coefficient Kv (or Cv in the British units).
The total pressure loss (in meters of water) is

Where Ploss - total pressure loss in the vessels connections, meters of water, Feed, Brine - total flow rates of feed and brine in the row, m3/hour; Kvf, Kvb - flow coefficients for feed manifold-to-vessel connection and the brine vessel-to-manifold one.
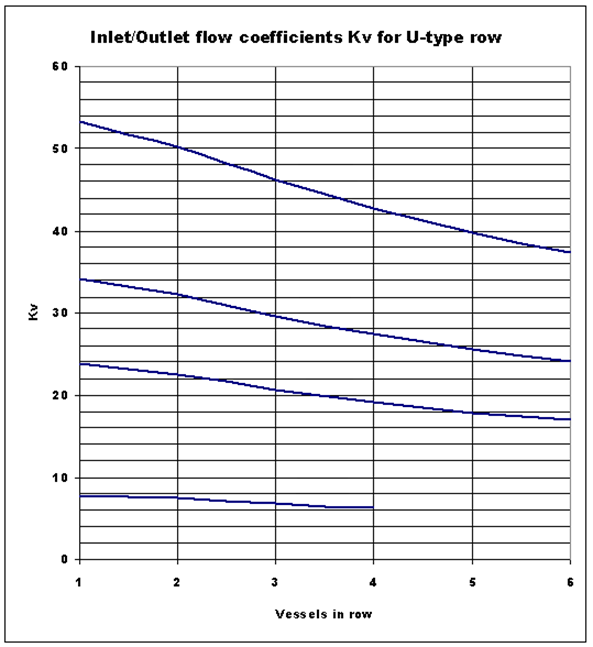
The Kvf and Kvb values are read from the graph below (Fig.6) built for ANSI schedule 80 ports). For the 60 and 40 schedules the Kv values are bigger by 5…10%.
The pressure loss calculation procedure may be summarized as follows.
- Define the feed and brine flow rates and pressures
- Select the number of vessels in a row
- Select the port sizes for brine and feed connections from table 1
- From graph in Fig.6 read the Kv coefficients for feed and brine connections
- Using equation (1) calculate pressure losses
Example
Let’s define the pressure loss for the vessel arrangement shown in Fig.1 containing 2 x 16 rows, three vessels in a row. The feed flow rate to a row is 25 m3/h and the brine flow rate is 13.8 m3/h. For 2.5" port and 3 vessels in a row the Kv value is 29.5. Therefore the pressure loss is 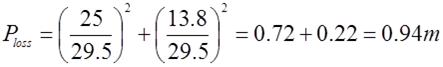
The required manifold minimum inner diameter can be derived from the equation (1).
As per ANSI B36.10 the nominal pipe size of 14 inch has inner diameter of 319mm. This size is a good choice for the manifold construction.
